Critical Phenomena in General Relativity
Consider the Einstein-scalar field equations for the spherically symmetric metric
![]()
for which hypersurfaces ![]() are out-going null cones having their vertices at
are out-going null cones having their vertices at ![]() . In these coordinates, an inertial observer is tracing the vertices of the outgoing null cones. The Minkowski spacetime of such inertial observer is given by
. In these coordinates, an inertial observer is tracing the vertices of the outgoing null cones. The Minkowski spacetime of such inertial observer is given by ![]() and
and ![]() . The illustration below shows how the inertial coordinate system at the origin remains connected with a coordinate system at infinity, e.g. in the limit
. The illustration below shows how the inertial coordinate system at the origin remains connected with a coordinate system at infinity, e.g. in the limit ![]() , during a time evolution when choosing different initial data for the scalar field. In deed, it is seen that spacetime evolves either to a Minkowski spacetime (i.e. is connected with an infinite observer) or to a black hole spacetime (i.e. has no connection with an infinite observer) depending on the value of the initial data parameter
, during a time evolution when choosing different initial data for the scalar field. In deed, it is seen that spacetime evolves either to a Minkowski spacetime (i.e. is connected with an infinite observer) or to a black hole spacetime (i.e. has no connection with an infinite observer) depending on the value of the initial data parameter ![]() .
.
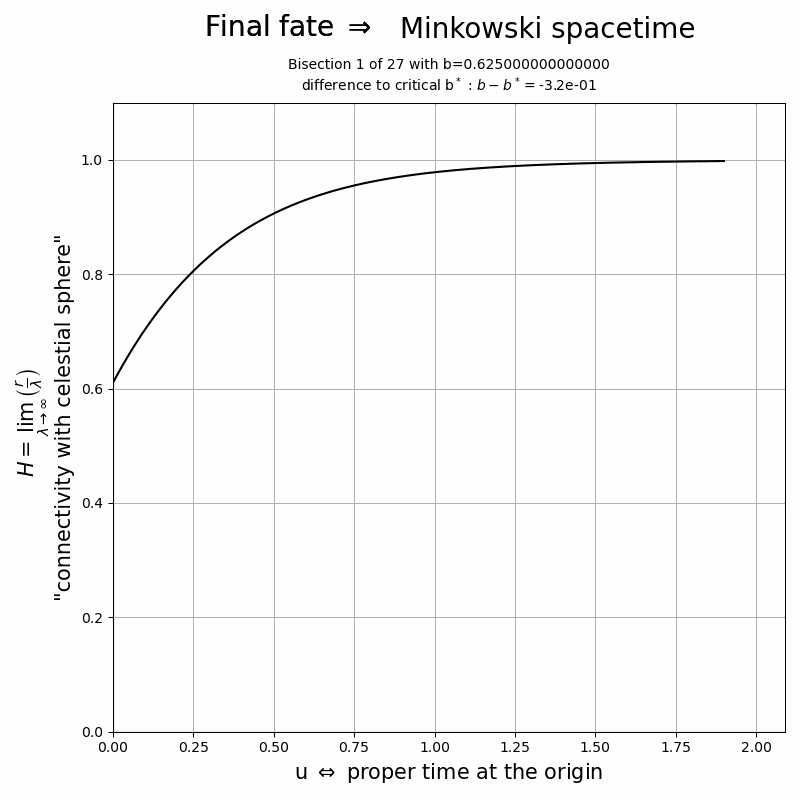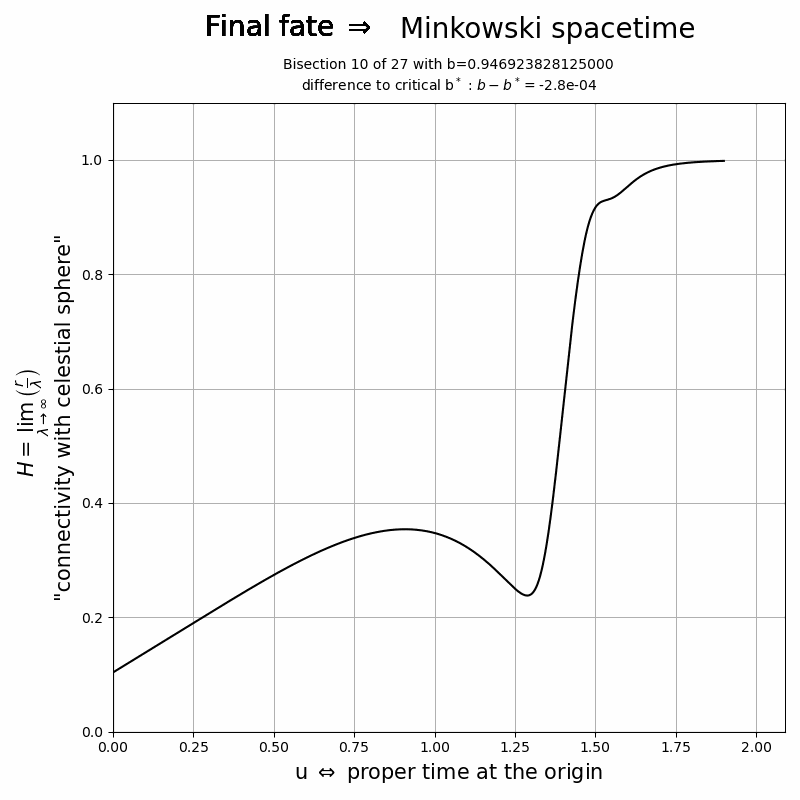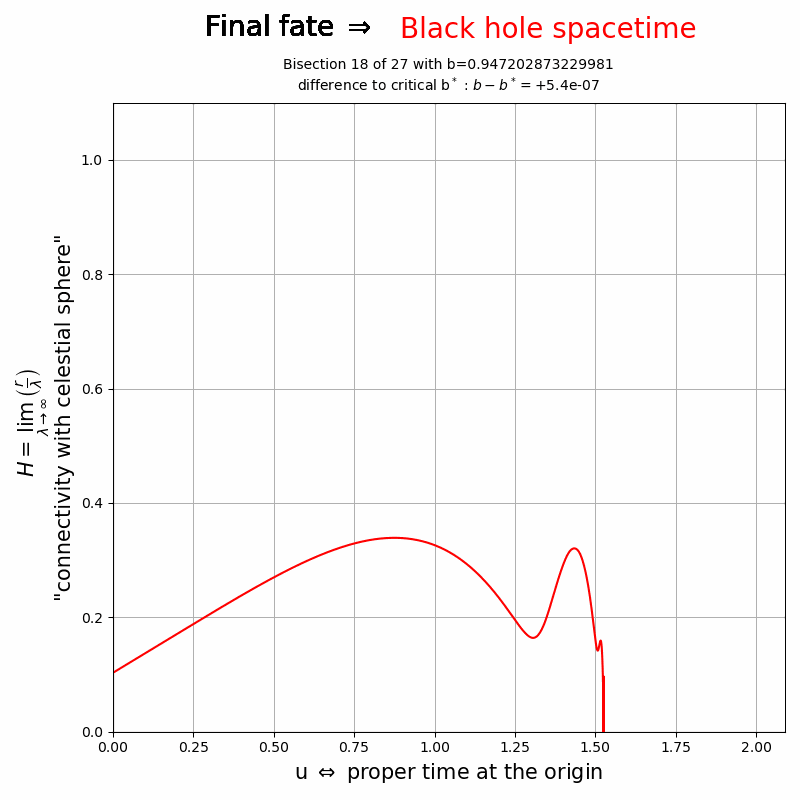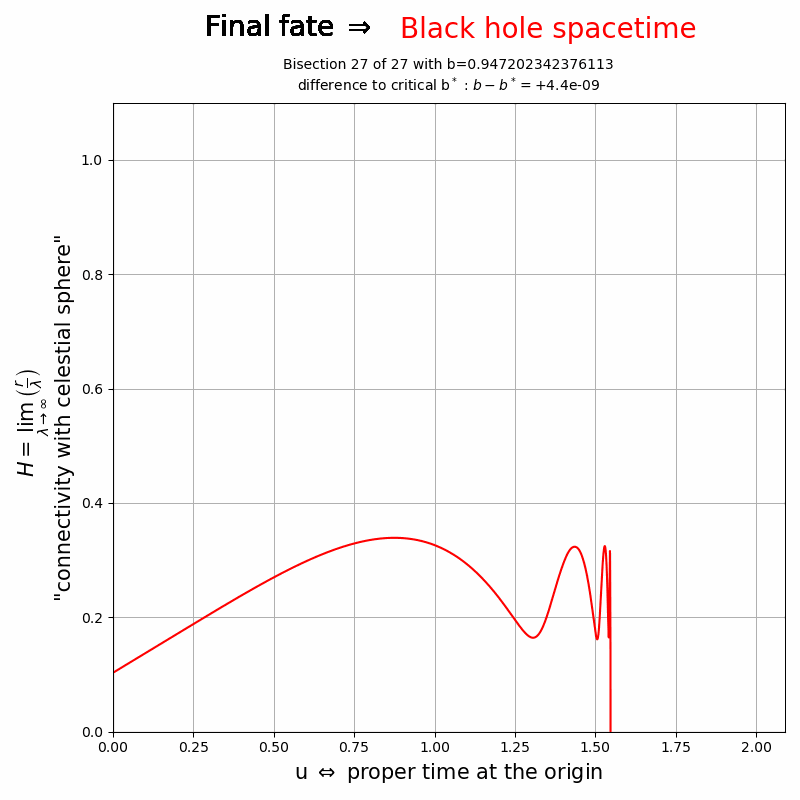
Temporal behaviour of ![]() for different values of the initial data and as a function of the proper time at the origin. Values
for different values of the initial data and as a function of the proper time at the origin. Values ![]() correspond to an asymptotic Minkowski frame while
correspond to an asymptotic Minkowski frame while ![]() indicates that the observer at large radii is hidden behind an event horizon. It also becomes apparent that for values of
indicates that the observer at large radii is hidden behind an event horizon. It also becomes apparent that for values of ![]() very close to a critical value
very close to a critical value ![]() , the field
, the field ![]() for times
for times ![]() is the same for both the Minkowski or black hole fate of the spacetime. This time
is the same for both the Minkowski or black hole fate of the spacetime. This time ![]() is the so-called critical collapse/dispersion time of the scalar field. Its value,
is the so-called critical collapse/dispersion time of the scalar field. Its value, ![]() , depends on the initial data, but the shape of
, depends on the initial data, but the shape of ![]() for
for ![]() is universally same for any(!) initial data.
is universally same for any(!) initial data.