In 1915 Einstein predicted a hitherto unknown form of radiation while linearising his newly derived theory of General Relativity. These gravitational waves are the only propagating degrees of freedom of a spacetime and they are generated by time-varying quadrupoles such as, supernovas or the merger of compact objects (black holes, neutron stars, white dwarfs).

Their wave character is different to sound waves which are propagating density perturbations in a medium as well as they are different to electromagnetic radiation which are oscillating electric and magnetic fields. Considering the multipole structure of the waves at far distances from the emitter, the former’s lowest order multipole is a monopole, meaning a time varying scalar function, while the latter is a dipole which is a three dimensional vector with time-varying components. The gravitational waves at large distances are quadrupole waves which can be expressed by a three times three matrix with time-varying components.

It took almost exactly 100 years to measure these waves in 2015. This is mainly because they have tiny amplitudes due to the large distance of the sources to a terrestrial observer. The gravitational wave observatories of the LIGO/Virgo consortium as well as the new Asian gravitational wave detector KAGRA are technological masterpieces and adopted most optimally measure quadrupolar deformation of spacetime itself. The detectors are L-shaped interferometers measuring to the distances between free-floating test masses at the ends of the L and its vertex. If a gravitational wave passes through the detector the relative distances between the test masses start to vary. Initially coherent light beams aligned between the test masses become phase shifted as an effect of the relative position change and this change is detected as gravitational wave.

However, not only the gravitational wave is measured during the passage of the wave through the detector. Another effect, although tiny, is recorded – a gravitational wave memory. This memory is a time integrated effect in the detector.

The gravitational wave memory effect can be roughly understood with the following 3-stage scenario:

• imagine test masses placed a the corners of an isosceles rectangular triangle and there is no gravitational wave
• a gravitational wave passes through the spacetime embedding test masses and changes continuously their position
• the gravitational wave abrupt stops and the test masses stop moving around.

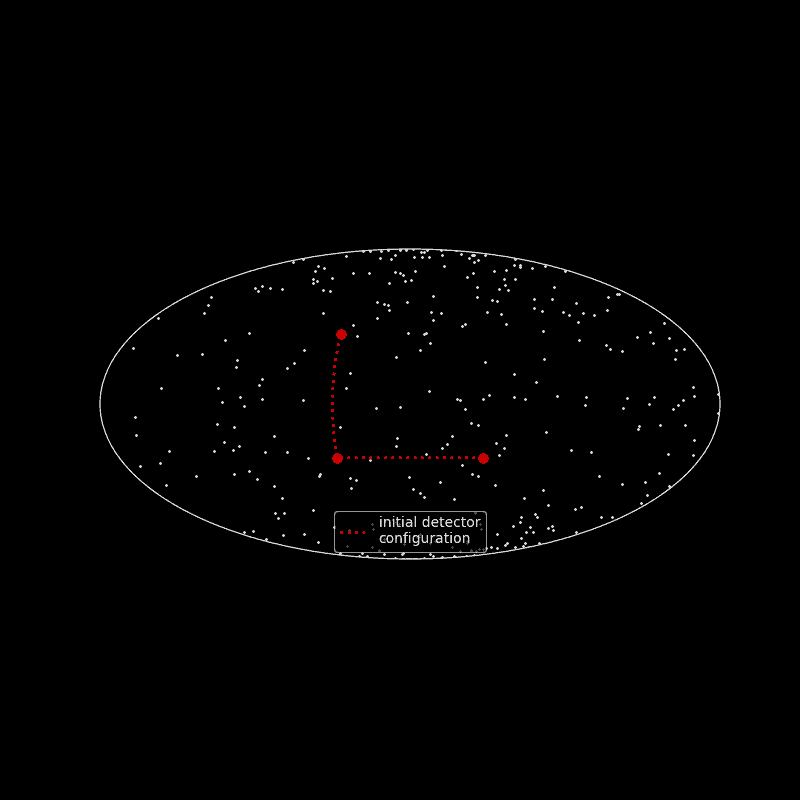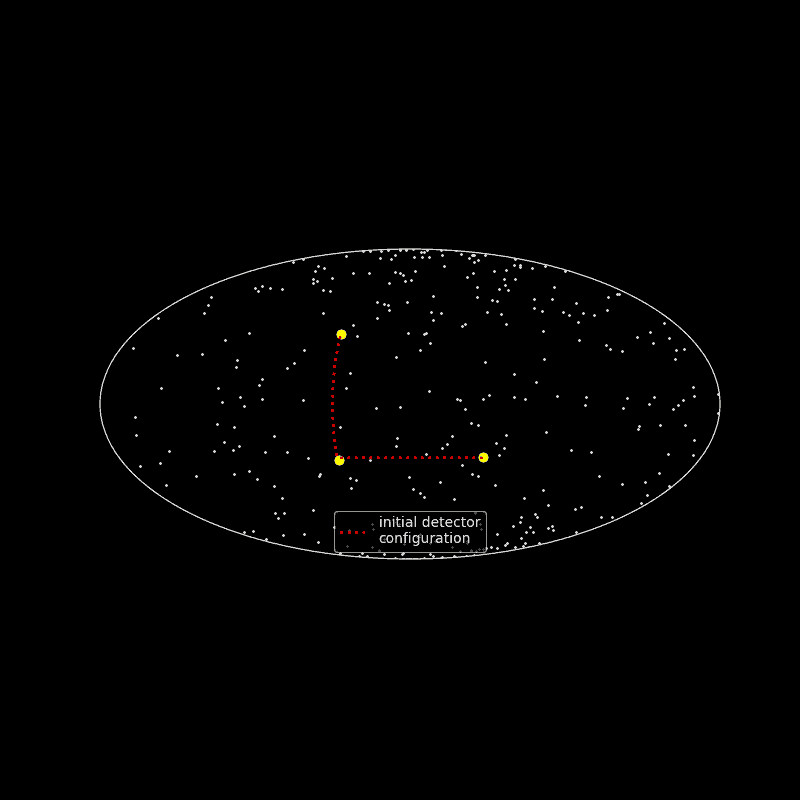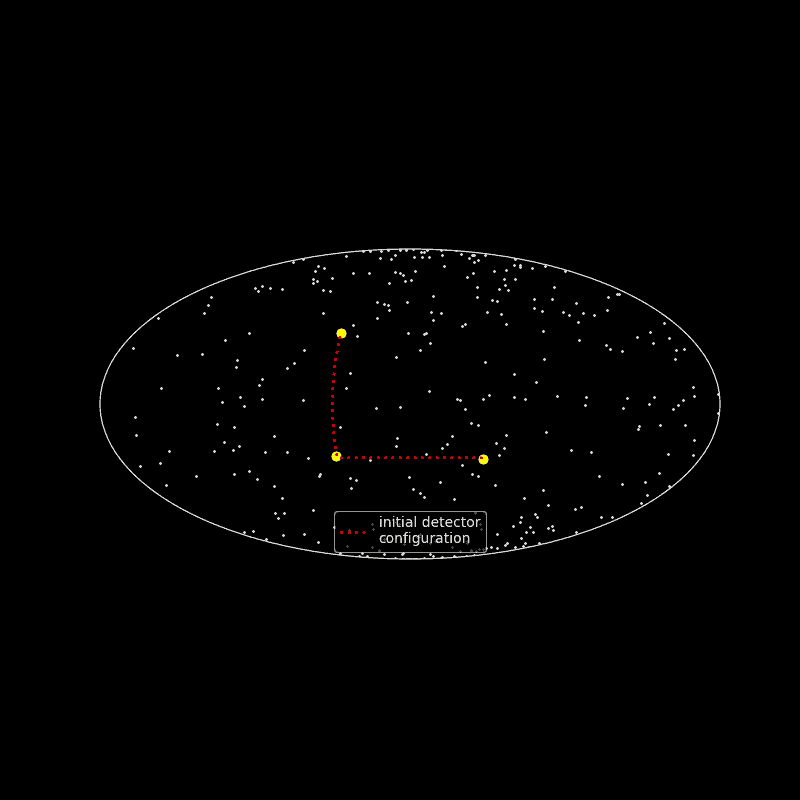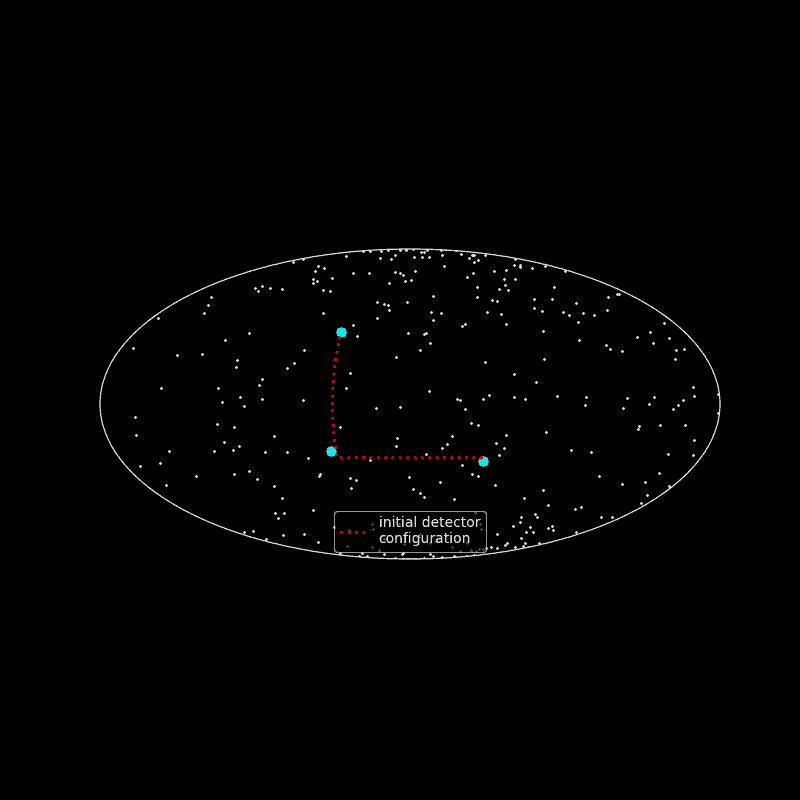
In the end the test masses do not reach their initial positions, where they formed an isosceles rectangular triangle. This change of permanent position is called the gravitational wave memory. The gravitational wave memory effect was independently found by Russian scientists Polnarev and Zeldovic in 1974 and American researchers Braginsky and Thorne in 1987. Currently the memory effect cannot be detected with present gravitational wave detectors because of the short time scale a gravitational wave needs to pass through the detector. Multiple passages of gravitational waves through the detector are needed to make a significant statistically measurable effect.

I am working in aspects of the gravitational wave memory effects in black hole spacetimes and relations to asymptotic symmetries and angular momentum. My work is supported with the Chilean National ANID grant FONDECYT de iniciación No 11190854. Relevant publications on the memory effect together with Jeff Winicour are

• Kerr black holes and nonlinear radiation memory, Classical and Quantum
  Gravity, Volume 36, Issue 9, article id. 095009 (2019)
• Boosted Schwarzschild metrics from a Kerr-Schild perspective,
  Classical and Quantum Gravity, Volume 35, Issue 3, article id. 035009
  (2018)
• Radiation memory, boosted Schwarzschild spacetimes and
  supertranslations, Classical and Quantum Gravity, Volume 34, Issue 11,
  article id. 115009 (2017)
• The sky pattern of the linearized gravitational memory effect,
  Classical and Quantum Gravity, Volume 33, Issue 17, article id. 175006
  (2016)

During the Fondecyt iniciación, I have developed a numerical code to solve the Einstein equations.

[\latexpage]Einstein equations, i.e the equations describing the interaction between spacetime geometry and matter, are a set of complicated partial differential equations with respect to a time coordinate and space coordinates parameterising the distance function, i.e. the metric of spacetime, and the matter variables (for example a scalar field).
Solving these equations analytically is in general not possible and numerical methods need to be employed.
In such a numerical setup, the solution of the partial differential equations require the specification of initial data.
In the null-cone formulation of General Relativity (which were used in this Fondecyt project) these initial data are free of any constrains.

One can now set up a family of initial data, say a family of bell-shaped profiles with different initial amplitude. Mathematically, speaking this a one-parametric family (because only the amplitude changes between different types of initial data) of initial data depending on a parameter, say $b$. It turns out there is a critical value $b^*$ with the following nature: if an initial data parameter $b$ is smaller than $b^*$ then the end product of the numerical evolution of the spacetime matter system is a flat space with all matter dispersed. But if the initial data parameter $b$ is bigger than $b^*$ then the end product will be a black hole spacetime with a singularity. This is the so–called critical phenomena of General Relativity, which serves as a test case for testing the validity of a numerical relativity simulation. An animated gif made from the numerical relativity code developed during this project and showing this critical behaviour can be found here.